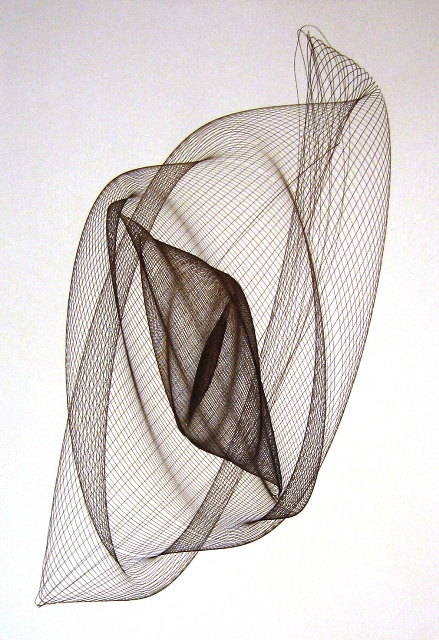
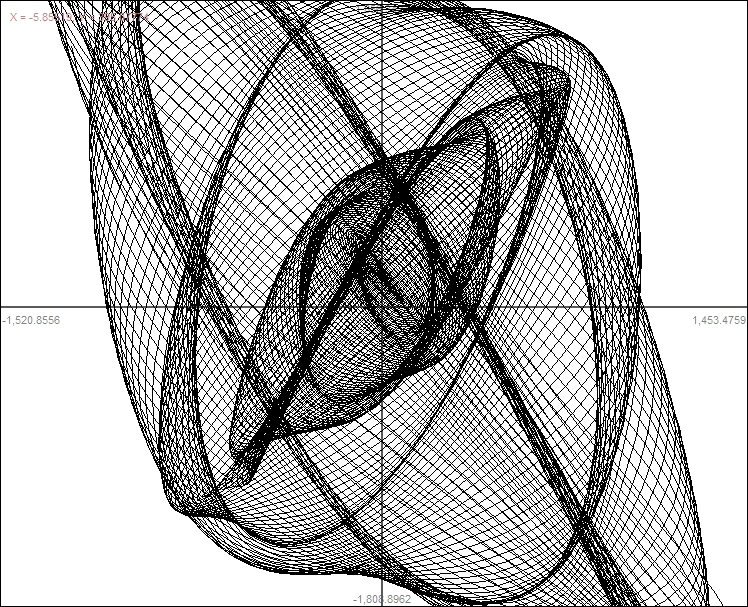
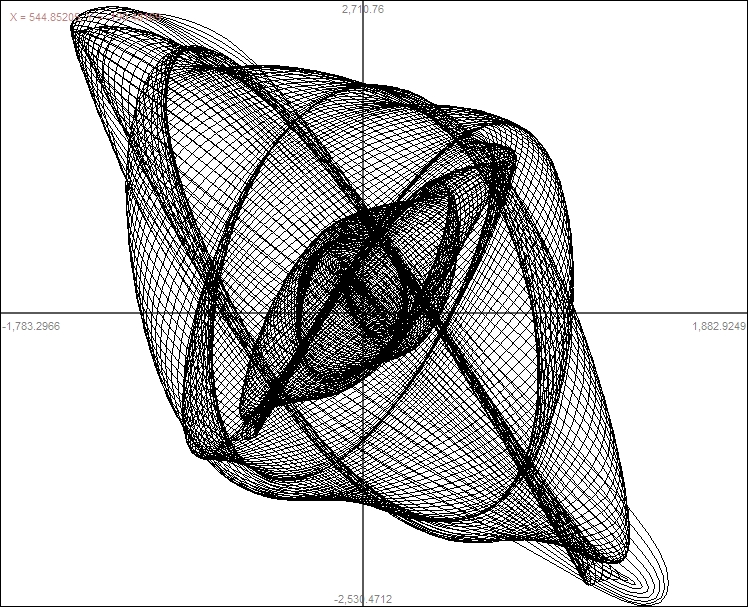
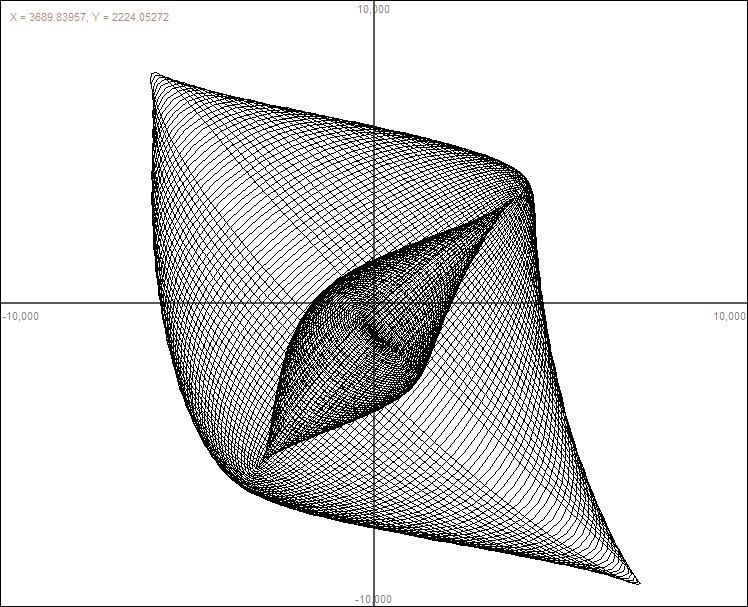
|
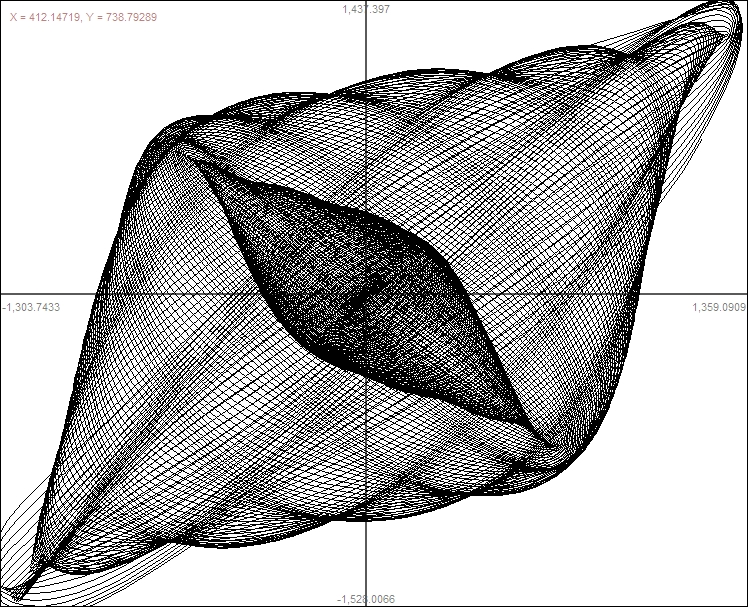
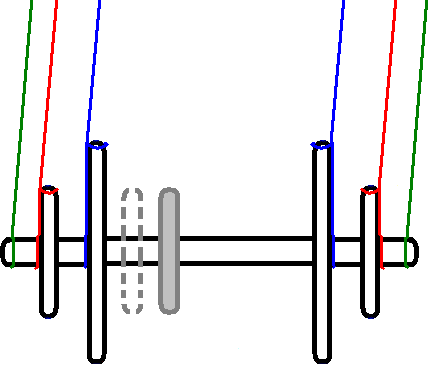
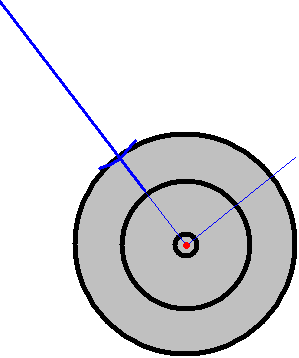
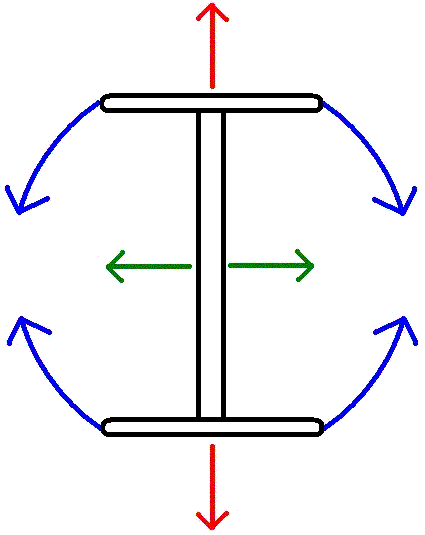
When the pendulum swings in a direction perpendicular to the barbell, as
shown in the middle graphic below (and with the green arrows in the graphic at
the right), the
effective radius for measuring period is the red
point (center of mass).When the pendulum swings parallel to the barbell
as shown in the left graphic (and with the
red arrows in graphic at the right), the effective radius is
the distance to the point where the string is tied. These two
different radii result in two different values for period, one for the
x component and one for the y component.
What I call a “third oscillation,” is found in the
twisting of the pendulum shown by the blue
arrows in the graphic at the right and determined by the moment of inertia of the
barbell along a vertical axis. The third oscillation was tuned to have a
period that was a multiple of one of the other periods to make for a
good drawing.
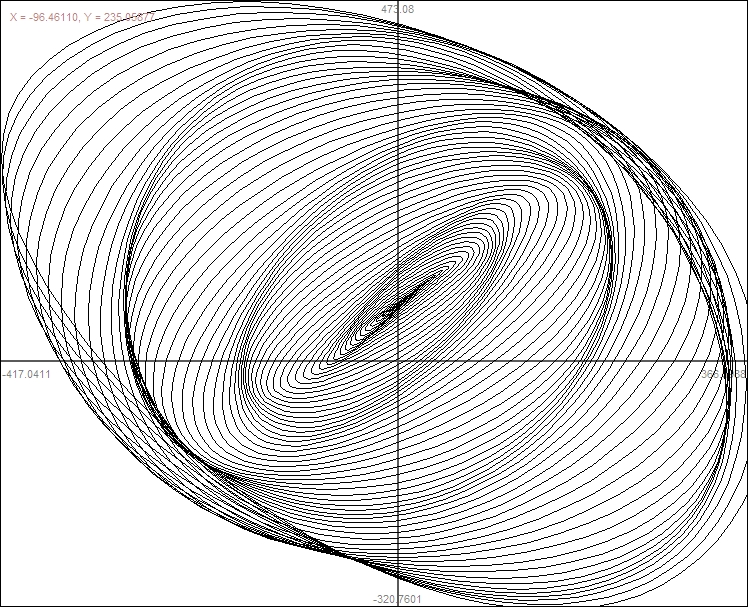
Friction between the pen and paper is assumed to be the main
source of damping. Since the friction force is independent of
velocity damping will be constant.
A More Mathematical Analysis:
Call the red arrows the y axis and the green arrows the x axis.
Since the pendulum is oscillating approximately harmonically it can be
described by the following parametric equation:
b=(close to zero); multiply by (k*t) for damping; a=amplitude;
x(t)=a*cos(t*b)(k*t)
y(t)=a*cos(t)(k*t)
Some people say the damping should be logarithmic. I think it
should be linear because the main source of damping (kinetic friction of
the pen sliding on the paper) is constant regardless of amplitude and
velocity. I cannot calculate the damping by the ladder.
Note: It's a good idea to have 't' go from negative to zero.
This way the thing slows to a stop. That is the type of
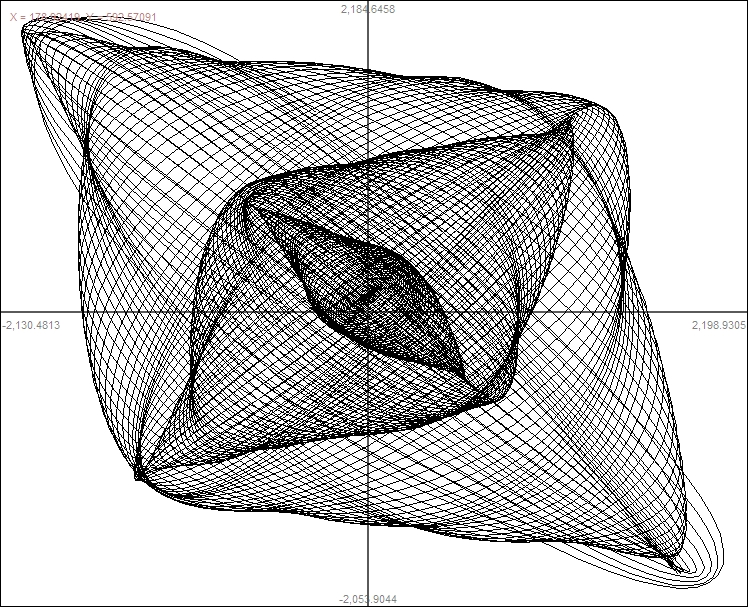
pictures drawn in the museum. My contraption was more complicated
because it also oscillated along the blue arrows. Unlike the
others, the period of this oscillation depends mostly on the moment of
inertia of the weights along a vertical axis. I could change 'I'
easily and very precisely by moving some smaller weight further or
closer to the center (see the gray weight in the first figure). It
was convenient to set this oscillation to be around twice the other
oscillations.
Assuming that the Blue arrow oscillation is harmonic (like a normal
pendulum it is not, but very close at small angles) then the angle 's'
that the pen will move is:
f=(constant, depends on 'I', f is almost 2);
j=damping
(Note: this motion was somewhat less damped by the
ladder than the green and red, so it gets its own constant);
s(t)=cos(t*f)*(j*t)
When the green and red arrows are zero:
r=(distance from center to pen); m=(amplitude);
y(t)=r*sin(cos(t*f)(j*t))m
x(t)=r*cos(cos(t*f)(j*t))m
To get the complicated motion simply add these to the original
parametric formula.
x(t)=a*cos(t*b)(k*t)+r*cos(cos(t*f)(j*t))m
y(t)=a*cos(t)(k*t)+r*sin(cos(t*f)(j*t))m
So to get different output, I simply tied the string to a different
weight (thus changing 'b') or moved the small weight around (changing
'f').
|