Catenary demonstration experiment, run with hyperbolic cosine
This experiment was
first performed for the NJIT Mathclub in Spring 2006.
Since then it has been a calculus project for students at Mount Rainier Lutheran High, WA where its hung in their commons. A number of other students from around the world have also demonstrated it.

Look carefully, the green line shows that all the white strings come down the the same height. This was done without rulers, calculators or numbers (and without cutting the rope afterwards)

A bit of geometric calculus shows that this trick works. Sorry I haven't completed a nice write-up. I have a crude email explanation I can forward to you if you contact me.

Changing the shape of the catenary. Notice the strings are longer here ('a' is larger). This was actually done first, then the strings quickly shortened for part II.

The catenary is less sharp here for the longer strings to line up. The levelness is easily seen next to the blackboard.
The two white strings that are smaller demonstrate that the density of the rope does not effect the shape it takes when it hangs.

Ravdeep Rana explains a few things on the board.

Image courtesy of Mathworld. More projects →
Since then it has been a calculus project for students at Mount Rainier Lutheran High, WA where its hung in their commons. A number of other students from around the world have also demonstrated it.
If you repeat this experiment or have questions, I would love to hear it, please contact me here.
Thanks
to all who came by to help and/ or spectate; the experiment was a
success.
Special thanks to Jeanina for taking some photos.

Look carefully, the green line shows that all the white strings come down the the same height. This was done without rulers, calculators or numbers (and without cutting the rope afterwards)

A bit of geometric calculus shows that this trick works. Sorry I haven't completed a nice write-up. I have a crude email explanation I can forward to you if you contact me.

Changing the shape of the catenary. Notice the strings are longer here ('a' is larger). This was actually done first, then the strings quickly shortened for part II.

The catenary is less sharp here for the longer strings to line up. The levelness is easily seen next to the blackboard.

The two white strings that are smaller demonstrate that the density of the rope does not effect the shape it takes when it hangs.

Ravdeep Rana explains a few things on the board.
Links about y=a*cosh(x/a)
Catenary curves, the shape that a hanging rope makes. Wikipedia. Heres a nice derivation of the hanging cable property.
Printable Directions:
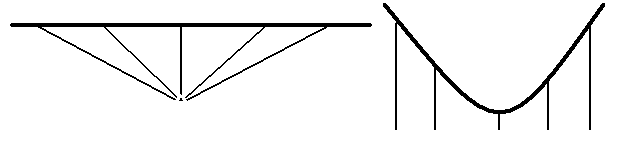
Imagine the dark line is a
heavy rope, the light lines are also some kind of rope. We set
everything as shown on the left, then hang the rope and then
surprisingly all the lines will line up straight at the bottom!
Room for Improvement:
- My proof is only geometric; we know let me know if you come up with an elegant complex variables proof (I expect that there is probably a one-liner proof out there).
-
The length of a catenary is proportional to both
its area and its derivative. Try and devise a
quick way to measure either- say if the curve is
drawn on a blackboard.

Image courtesy of Mathworld. More projects →